Balken met een gedeeltelijke verdeelde belasting

Roark's Formules voor Spanningen
Afschuiving, moment, helling, doorbuiging van elastische rechte balken-tabel 8.1
W=belasting (N), w=lijnbelasting (N/mm), M0=aanwezig moment (Nmm), θ0=hoeksverdraaiing (graden),
RA en RB zijn de verticale eindreacties, respectievelijk links en rechts (N),
MA and MB zijn de eindmomenten, respectievelijk links en rechts (Nmm)

2. Gedeeltelijk verdeelde belasting

Lijnbelasting wa (N/mm):
Lijnbelasting wl (N/mm):
Afstand l (mm):
Afstand a (mm):
E-modulus E (MPa):
Traagheidsmoment I (Nmm4):
Afstand van de neutrale vezel tot de uiterste vezel v (mm):

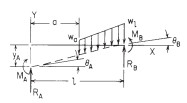2a. Linkerkant vrij, rechterkant vast (uitkragende ligger)

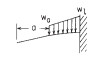RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	σA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

Max M = MB (Nmm):	maxM
Max σ = σB (MPa):	maxσ
Max θ = θA (graden):	Maxθ
Max y = yA (mm):	maxY

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

Max M = MB (Nmm):	maxM
Max σ = σB (MPa):	maxσ
Max θ = θA (graden):	Maxθ
Max y = yA (mm):	maxY

Als a=0 en wl = 0 (gelijkmatige afnemende belasting)

Max M = MB (Nmm):	maxM
Max σ = σB (MPa):	maxsigma
Max θ = θA (graden):	Maxθ
Max y = yA (mm)	maxY

2b. Linkerkant geleid, rechterkant vast

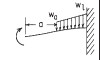RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	σA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

Max -M = MB (Nmm):	max-M
Max -σ = σB (MPa):	max-σ
Max +M = MA (Nmm):	max+M
Max +σ = σA (MPa):	max+σ
Max y = yA (mm):	maxY

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

Max -M = MB (Nmm):	max-M
Max -σ = σB (MPa):	max-σ
Max +M = MA (Nmm):	max+M
Max +σ = σA (MPa):	max+σ
Max y = yA (mm):	maxY

Als a=0 en wl = 0 (gelijkmatige afnemende belasting)

Max -M = MB (Nmm):	max-M
Max -σ = σB (MPa):	max-σ
Max +M = MA (Nmm):	max+M
Max +σ = σA (MPa):	max+σ
Max y = yA (mm):	maxY

2c. Linkerkant vrije oplegging, rechterkant vast

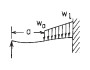RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	σA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

RA (N):	RA	RB (N):	RB
Max +M (Nmm):	max+M	waar x (mm) =	x
Max -M = MB (Nmm):	max-M	Max -σ = σB (MPa):	max-σ
Max +σ (MPa):	max+σ	Max θ = θA (graden):	maxθ
Max y (mm)	maxY	waar x (mm) =	x

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

RA (N):	RA	RB (N):	RB
Max +M (Nmm):	max+M	waar x (mm) =	x
Max -M = MB (Nmm):	max-M	Max -σ = σB (MPa):	max-σ
Max +σ (MPa):	max+σ	Max θ = θA (graden):	maxθ
Max y (mm)	maxY	waar x (mm) =	x

Als a=0 en wl = 0 (gelijkmatige afnemende belasting)

RA (N):	RA	RB (N):	RB
Max +M (Nmm):	max+M	waar x (mm) =	x
Max -M = MB (Nmm):	max-M	Max -σ = σB (MPa):	max-σ
Max +σ (MPa):	max+σ	Max θ = θA (graden):	maxθ
Max y (mm)	maxY	waar x (mm) =	x

2d. Linkerkant vast, rechterkant vast

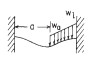RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	σA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

Max +M (Nmm):	max+M	waar x (mm) =	x
Max -M = MA=MB (Nmm):	max-M	Max -σ = σA= σB (MPa):	max-σ
Max +σ (MPa):	max+σ
Max y (mm)	maxY	waar x (mm) =	x

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	σA (MPa):	σA
Max +M (Nmm):	max+M	waar x (mm) =	x
Max -M = MB (Nmm):	max-M	Max -σ = σB (MPa):	max-σ
Max +σ (MPa):	max+σ
Max y (mm)	maxY	waar x (mm) =	x

2e. Linkerkant vrije oplegging, rechterkant vrije oplegging

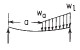RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	sigmaA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

RA (N):	RA	RB (N):	RB
Max M (Nmm):	maxM	waar x (mm) =	x
Max σ (MPa):	maxσ	Max θ = θB (graden)	maxθ
Max y (mm):	maxY	waar x (mm)=	x

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

RA (N):	RA	RB (N):	RB
Max M (Nmm):	maxM	waar x (mm) =	x
Max σ (MPa):	maxσ
Max θ = θA (graden)	maxθ	Max θ = θB (graden)	maxθ
Max y (mm):	maxY	waar x (mm)=	x

2f. Linkerkant geleid, rechterkant vrije oplegging

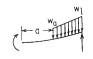RA (N):	RA	RB (N):	RB
MA (Nmm):	MA	MB (Nmm):	MB
σA (MPa):	σA	σB (MPa):	σB
θA (graden):	θA	θB (graden):	θB
doorbuiging yA (mm):	yA	doorbuiging yB (mm):	yB

Als a=0 en wl = wa (uniforme belasting over de volledige lengte)

Max M = MA(Nmm):	maxM
Max σ = σA(MPa):	maxσ
Max θ = θB (graden)	maxθ
Max y = yA(mm):	maxY

Als a=0 en wa = 0 (gelijkmatige toenemende belasting)

Max M = MA(Nmm):	maxM
Max σ = σA(MPa):	maxσ
Max θ = θB (graden)	maxθ
Max y = yA(mm):	maxY

Als a=0 en wl = 0 (gelijkmatige afnemende belasting)

Max M = MA(Nmm):	maxM
Max σ = σA(MPa):	maxσ
Max θ = θB (graden)	maxθ
Max y = yA(mm):	maxY