| Roark's Formulas for Stress and Strain |
|---|
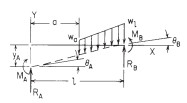
| Shear, moment, slope, deflection of elastic straight beams-table 8.1 |
| W=load (N), w=unit load (N/mm), M0=applied couple (Nmm), θ0=angular displacement (degrees), |
| RA and RB are the vertical end reactions at left and right respectively (N), |
| MA and MB are the reaction end moments at left and right respectively (Nmm) |
| 2. Partial distributed load |
|---|
 |
| 2a. Left end free, right end fixed (cantilever) |
|---|
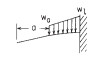 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | σA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| Max M = MB (Nmm): | maxM |
| Max σ = σB (MPa): | maxσ |
| Max θ = θA (degrees): | Maxθ |
| Max y = yA (mm): | maxY |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| Max M = MB (Nmm): | maxM |
| Max σ = σB (MPa): | maxσ |
| Max θ = θA (degrees): | Maxθ |
| Max y = yA (mm): | maxY |
| If a=0 and wl = 0 (uniformly decreasing load) |
|---|
| Max M = MB (Nmm): | maxM |
| Max σ = σB (MPa): | maxsigma |
| Max θ = θA (degrees): | Maxθ |
| Max y = yA (mm) | maxY |
| 2b. Left end guided, right end fixed |
|---|
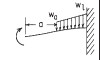 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | σA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| If a=0 and wl = wa (uniform load on the entire span) |
|---|
| Max -M = MB (Nmm): | max-M |
| Max -σ = σB (MPa): | max-σ |
| Max +M = MA (Nmm): | max+M |
| Max +σ = σA (MPa): | max+σ |
| Max y = yA (mm): | maxY |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| Max -M = MB (Nmm): | max-M |
| Max -σ = σB (MPa): | max-σ |
| Max +M = MA (Nmm): | max+M |
| Max +σ = σA (MPa): | max+σ |
| Max y = yA (mm): | maxY |
| If a=0 and wl = 0 (uniformly decreasing load) |
|---|
| Max -M = MB (Nmm): | max-M |
| Max -σ = σB (MPa): | max-σ |
| Max +M = MA (Nmm): | max+M |
| Max +σ = σA (MPa): | max+σ |
| Max y = yA (mm): | maxY |
| 2c. Left end simply supported, right end fixed |
|---|
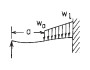 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | σA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| If a=0 and wl = wa (uniform load on the entire span) |
|---|
| RA (N): | RA | RB (N): | RB |
| Max +M (Nmm): | max+M | at x (mm) = | x |
| Max -M = MB (Nmm): | max-M | Max -σ = σB (MPa): | max-σ |
| Max +σ (MPa): | max+σ | Max θ = θA (degrees): | maxθ |
| Max y (mm) | maxY | at x (mm) = | x |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| RA (N): | RA | RB (N): | RB |
| Max +M (Nmm): | max+M | at x (mm) = | x |
| Max -M = MB (Nmm): | max-M | Max -σ = σB (MPa): | max-σ |
| Max +σ (MPa): | max+σ | Max θ = θA (degrees): | maxθ |
| Max y (mm) | maxY | at x (mm) = | x |
| If a=0 and wl = 0 (uniformly decreasing load) |
|---|
| RA (N): | RA | RB (N): | RB |
| Max +M (Nmm): | max+M | at x (mm) = | x |
| Max -M = MB (Nmm): | max-M | Max -σ = σB (MPa): | max-σ |
| Max +σ (MPa): | max+σ | Max θ = θA (degrees): | maxθ |
| Max y (mm) | maxY | at x (mm) = | x |
| 2d. Left end fixed, right end fixed |
|---|
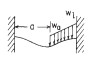 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | σA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| If a=0 and wl = wa (uniform load on the entire span) |
|---|
| Max +M (Nmm): | max+M | at x (mm) = | x |
| Max -M = MA=MB (Nmm): | max-M | Max -σ = σA= σB (MPa): | max-σ |
| Max +σ (MPa): | max+σ | ||
| Max y (mm) | maxY | at x (mm) = | x |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | σA (MPa): | σA |
| Max +M (Nmm): | max+M | at x (mm) = | x |
| Max -M = MB (Nmm): | max-M | Max -σ = σB (MPa): | max-σ |
| Max +σ (MPa): | max+σ | ||
| Max y (mm) | maxY | at x (mm) = | x |
| 2e. Left end simply supported, right end simply supported |
|---|
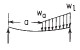 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | sigmaA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| If a=0 and wl = wa (uniform load on the entire span) |
|---|
| RA (N): | RA | RB (N): | RB |
| Max M (Nmm): | maxM | when x (mm) = | x |
| Max σ (MPa): | maxσ | Max θ = θB (degrees) | maxθ |
| Max y (mm): | maxY | when x (mm)= | x |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| RA (N): | RA | RB (N): | RB |
| Max M (Nmm): | maxM | when x (mm) = | x |
| Max σ (MPa): | maxσ | ||
| Max θ = θA (degrees) | maxθ | Max θ = θB (degrees) | maxθ |
| Max y (mm): | maxY | when x (mm)= | x |
| 2f. Left end guided, right end simply supported |
|---|
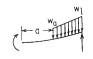 |
| RA (N): | RA | RB (N): | RB |
| MA (Nmm): | MA | MB (Nmm): | MB |
| σA (MPa): | σA | σB (MPa): | σB |
| θA (degrees): | θA | θB (degrees): | θB |
| deflection yA (mm): | yA | deflection yB (mm): | yB |
| If a=0 and wl = wa (uniform load on the entire span) |
|---|
| Max M = MA(Nmm): | maxM |
| Max σ = σA(MPa): | maxσ |
| Max θ = θB (degrees) | maxθ |
| Max y = yA(mm): | maxY |
| If a=0 and wa = 0 (uniformly increasing load) |
|---|
| Max M = MA(Nmm): | maxM |
| Max σ = σA(MPa): | maxσ |
| Max θ = θB (degrees) | maxθ |
| Max y = yA(mm): | maxY |
| If a=0 and wl = 0 (uniformly decreasing load) |
|---|
| Max M = MA(Nmm): | maxM |
| Max σ = σA(MPa): | maxσ |
| Max θ = θB (degrees) | maxθ |
| Max y = yA(mm): | maxY |




