| Charge de ligne due au poids propre de l’axe |
? |
N/mm |
| Longueur totale de l’axe |
? |
mm |
| |
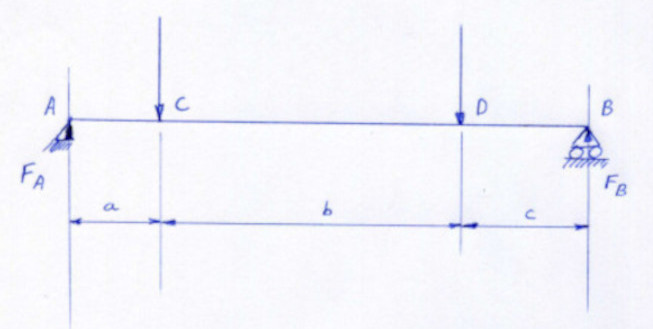
| T_A (force latérale en A) |
? |
N |
| T_C21 (force latérale 1 en C) |
? |
N |
| T_C22 (force latérale 2 en C) |
? |
N |
| T_D21 (force latérale 1 en D) |
? |
N |
| T_D22 (force latérale 2 en D) |
? |
N |
| T_B (force latérale en B) |
? |
N |
| Valeur la plus basse de T_A,T_C21,T_C22,T_D21, T_D22, T_B |
? |
N |
| Valeur la plus haute de T_A,T_C21,T_C22,T_D21, T_D22, T_B |
? |
N |
| |
| Force de réaction FA |
? |
N |
| Force de réaction FB |
? |
N |
| |
| Position avec le moment de flexion maximal |
? |
|
| Position du point zéro sur la ligne de force transversale |
? |
mm |
| Moment de flexion maximal |
? |
Nmm |
| |
| Déformation au milieu de l’axe |
? |
mm |
| Déflexion maximale sur l’ensemble de l’axe (40 points d’évaluation equidistants) |
? |
mm |
| Déflexion maximale sur tout l’axe à distance |
? |
mm |
| Limite de déflexion basée sur la longueur totale/300 |
? |
mm |
| |
| Le moment I sur v |
? |
mm3 |
| Diamètre d |
? |
mm |